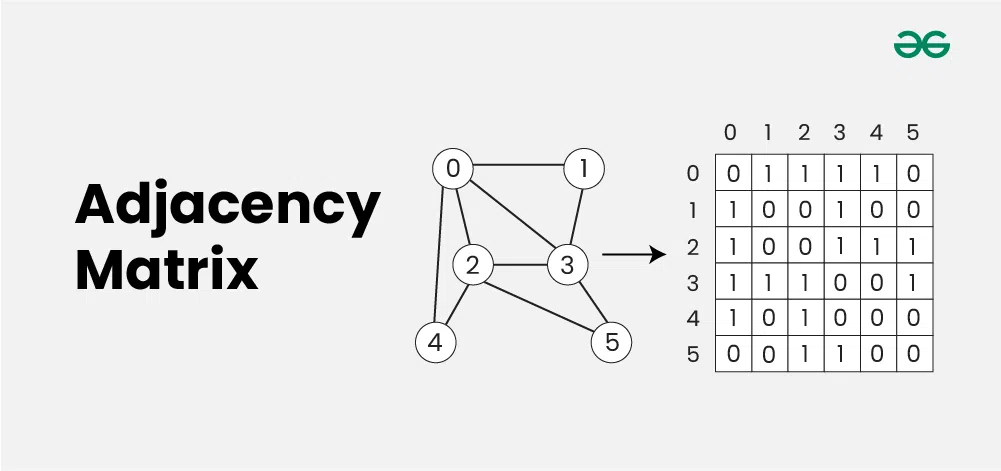
Definition:

An adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph.

Contruction:

• Vertices: Assume a graph G has n vertices.
• Matrix: The adjacency matrix A will be a n×n matrix
  • A[i][j]=1 if there is an edge from vertex i to vertex j.
  • A[i][j]=0 if there is no edge from vertex i to vertex j.

Types of Graphs and Adjacency Matrices:

1.Undirected Graph:

• The adjacency matrix is symmetric.
• A[i][j]=A[j][i]
• Example:
     A B C
  A 0 1 1
  B 1 0 0
  C 1 0 0

2.Directed Graph:

• The adjacency matrix is not necessarily symmetric.
• Example:
      A B C
  A 0 1 1
  B 0 0 0
  C 1 0 0

3.Weighted Graph:

• Instead of 1s and 0s, the matrix contains the weights of the edges.
• A[i][j]=w (weight of the edge) if there is an edge from i to j, otherwise 0 (or some other indication of no edge, such as infinity for algorithms like Dijkstra’s).
• Example:
      A B C
  A 0 2 3
  B 0 0 0
  C 1 0 0

4.Unweighted Graph:

• The adjacency matrix contains only 1s and 0s.
• Example:
      A B C
  A 0 1 1
  B 1 0 0
  C 1 0 0

Pros and Cons of Adjacency Matrix:

Pros

• Simple and Easy to Understand: Provides a clear visual representation of the graph.
• Efficient Edge Lookup: Checking for the existence of an edge between two vertices is O(1).
• Memory Efficiency for Dense Graphs: Efficient for graphs where the number of edges is close to the number of possible edges, n^2.

Cons

• Memory Inefficiency for Sparse Graphs: Requires O(n^2) space, which can be inefficient for graphs with few edges relative to the number of vertices.
• Edge Iteration Inefficiency: Iterating over all edges is O(n^2) which is inefficient for sparse graphs.